マテリアルズインフォマティクスに関わっていると、MDなど、計算科学的シミュレーションに関する話を聞くことも多い。

このとき、しばしばモンテカルロ法という言葉を聞いた。しかし、自分は実験系の出身で計算科学の知識に乏しく、手法のイメージがつかなかった。

これについて調べてみたところとても面白く、概念としてはわかりやすものだったので、ここに記しておく。

モンテカルロ法とは

Wikipediaによると以下。

シミュレーションや数値計算を乱数を用いて行う手法の総称。

モンテカルロ法 - Wikipedia

簡単に言えば、ランダムに発生させた数値を使ってその値を求めることをいう。

よくこれを直感的にもわかりやすく説明するために、円周率$\pi$を推算する例が挙げられる。

モンテカルロ法により円周率を求める

考え方

一辺の長さが$1$の正方形を考える。この正方形には半径$\frac{1}{2}$の円が内接している。

正方形の中にランダムに点を打つ場合、内接円の中に点が入る確率は正方形の面積と内接円の面積の比で表される。

したがって、この確率を$p$とすると円周率$\pi$を用いて以下のように表せる。

\[p = \frac{\mathrm{内接円の面積}}{\mathrm{正方形の面積}} = \frac{\pi \left( \frac{1}{2} \right)^2}{1 \times 1} = \frac{\pi}{4}\]

つまり、$\pi$はここで求めた確率の4倍（$4p$）で求めることができる。

この$p$を乱数によって求めようという考え方。

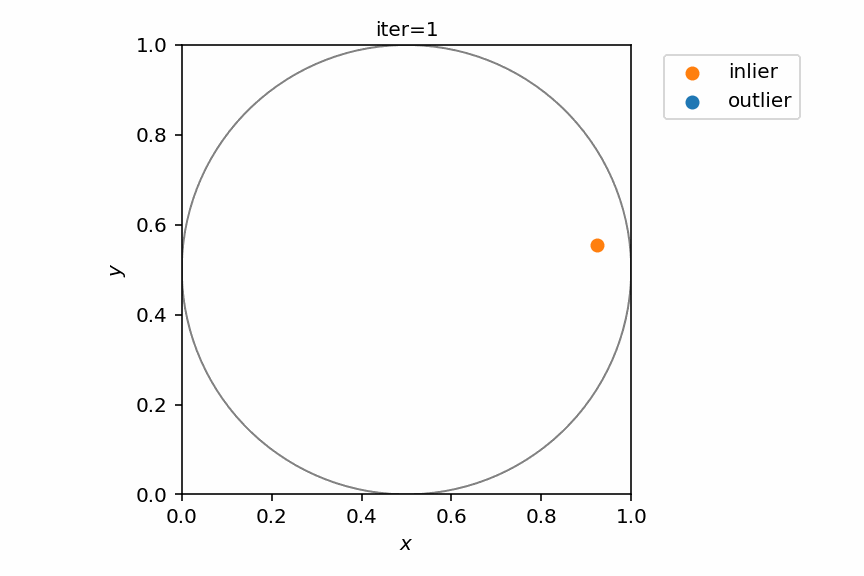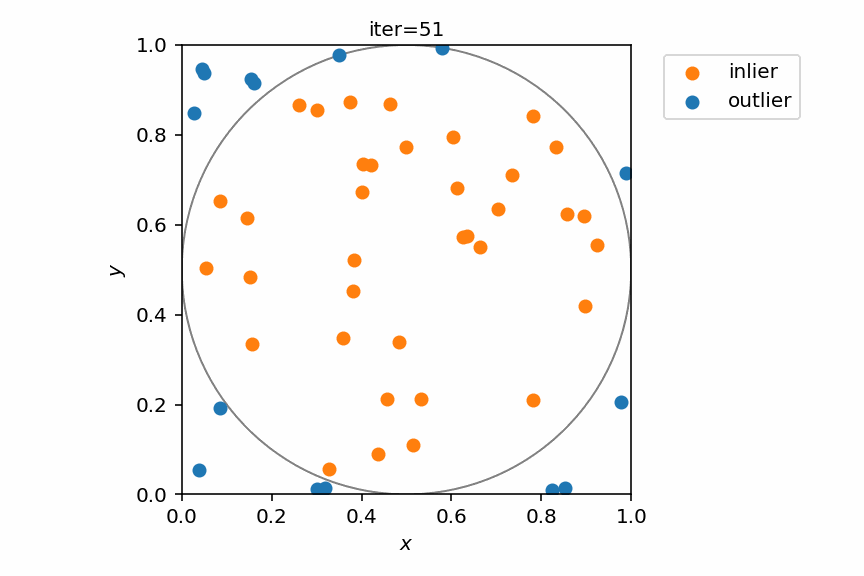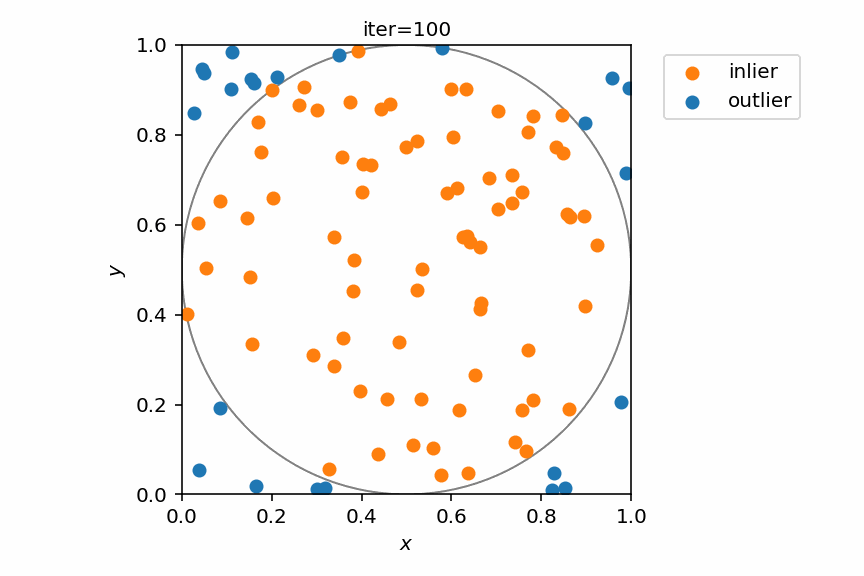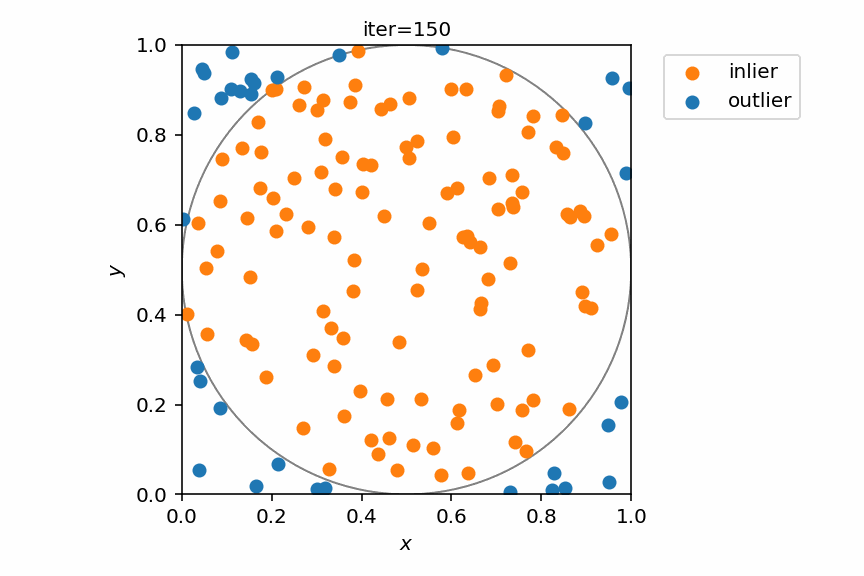
グラフ上でこの問題を考えるため、$xy$平面上の$(0,0), (0,1), (1,1), (1,0)$の4点を繋いだ正方形を想定する。

この場合、$x$座標$y$座標それぞれが、独立に0から1の一様分布に従った乱数を用いることで$p$の値を推算することができる。

Pythonによる実装

ランダムに100回点を打つ様子をPythonで実装してみる。

できる限り標準ライブラリを利用している。

import random
from time import time
import itertools
import math
import sys

import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib import animation
from matplotlib import patches

print(f'Python version: {sys.version}')
print(f'matplotlib version: {mpl.__version__}')

Python version: 3.9.13 | packaged by conda-forge | (main, May 27 2022, 17:01:00)
[Clang 13.0.1 ]
matplotlib version: 3.5.2

random.seed(334)

# 時間計算用
t1 = time()

# アニメーションのために何回分を描画するか
n_iteration_for_animation = 150

# figure, axisを作成
fig, ax = plt.subplots(facecolor='w', dpi=144)

# 内接円の描画
c = patches.Circle(xy=(0.5, 0.5), radius=0.5, facecolor='None', edgecolor='gray', zorder=0.5)
ax.add_patch(c)

# レイアウトを調整
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.set_aspect('equal')

# アニメーション用のリストを作成
ims = []        # アニメーション用のリスト
X_inlier = []   # 内接円に含まれる点のx座標
Y_inlier = []   # 内接円に含まれる点のy座標
X_outlier = []  # 内接円の外側の点のx座標
Y_outlier = []  # 内接円の外側の点のy座標

# 内接円の内側にプロットされたらTrue、外側にプロットされたらFalseを返したものを保存する。
flags_inlier:list[bool] = []
for iter in range(n_iteration_for_animation):
    x = random.random()
    y = random.random()
    flag_inlier = (x-0.5)**2 + (y-0.5)**2 <= 0.5**2
    if flag_inlier:
        X_inlier.append(x)
        Y_inlier.append(y)
    else:
        X_outlier.append(x)
        Y_outlier.append(y)
    flags_inlier.append(flag_inlier)
    im_title = title = ax.text(0.5, 1.01, f'iter={iter+1}', ha='center', va='bottom')
    im_inlier = ax.scatter(X_inlier, Y_inlier, c='C1', label='inlier')
    im_outlier = ax.scatter(X_outlier, Y_outlier, c = 'C0', label='outlier')
    ims.append([im_title, im_inlier, im_outlier])

ax.legend(handles=[im_inlier, im_outlier], bbox_to_anchor=(1.05, 1))
fig.tight_layout()

ani = animation.ArtistAnimation(fig, ims, interval=100)
ani.save('monte-carlo-simulation-pi.gif', writer='pillow')
t2 = time()
print(f'Time: {t2-t1:.2f} sec')

Time: 10.69 sec

ax.clear()
plt.close()

p = sum(flags_inlier) / n_iteration_for_animation
print(f'p = {p:.2f}')
print(f'piの推算値: {4*p:.2f}')

p = 0.78
piの推算値: 3.12

この時点である程度いい感じに推算できている。

続きからやって1,000,000回 （100万回）やってみる。

n_iteration = 1_000_000
for iter in range(n_iteration_for_animation, n_iteration):
    x = random.random()
    y = random.random()
    flag_inlier = (x-0.5)**2 + (y-0.5)**2 <= 0.5**2
    flags_inlier.append(flag_inlier)

推算の過程を描画する。

全体と最初の部分を抽出したものの二種類を描画する。

# 累積和を利用して確率pを計算。それを4倍してpiを計算
lst_pie_estimated:list[float] = [4*n_inlier/(n_iter+1) for n_iter, n_inlier in enumerate(itertools.accumulate(flags_inlier))]

# syle
mpl.style.use('seaborn-darkgrid')

# figure, axisを作成
fig, axes = plt.subplots(2, 1, figsize = (6.4, 9.6), facecolor='w', dpi=144)
for j, _range in enumerate(((0, n_iteration), (0, int(0.05*n_iteration)))):
    ax:plt.Axes = axes[j]

    # xの範囲を手動で設定するため、計算する
    alpha = 0.05
    offset = (_range[1] - _range[0]) * alpha
    range_xlim = (_range[0] - offset, _range[1] + offset)

    # 正しいpi
    ax.plot(range_xlim, [math.pi]*len(range_xlim), c = 'gray', linestyle = '--', label='$\pi$')
    # 推算したpi
    ax.plot(range(*_range), lst_pie_estimated[slice(*_range)], label='estimated $\pi$')

    # layout
    if j == 0:
        ax.set_title(f'Random simulation (n = {n_iteration})')
    else:
        ax.set_title(f'{min(_range)+1} to {max(_range)}')
    ax.set_xlim(range_xlim)
    ax.set_xlabel('iteration')
    ax.set_ylabel('$\pi$')
    ax.legend()
fig.tight_layout()

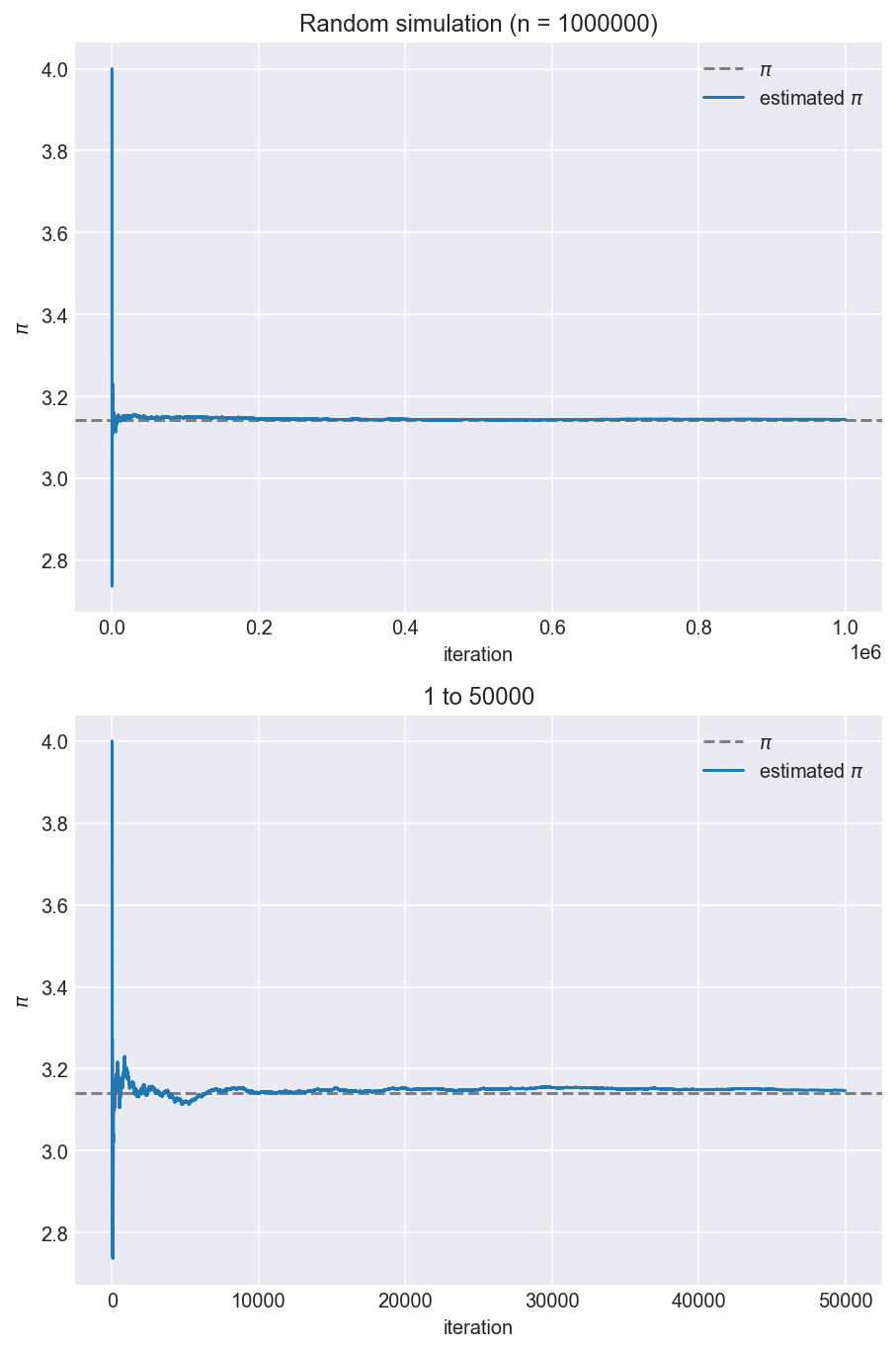
シミュレーションの終了後推算した値を求めると以下。

print('実際の値: {:.5f}'.format(math.pi))
print('推算値: {:.5f}'.format(4*sum(flags_inlier)/n_iteration))

実際の値: 3.14159
推算値: 3.14382

ある程度推算できていることがわかる。

コメント

分子動力学法などで用いられるモンテカルロ法とは異なる部分も多いと思うが、この例を思い出すことである値を推算するための手法であると理解できて安心できる、気がする。

自分で動かせる方はシード値を変えて試してみると面白いと思う。

関連

https://note.yu9824.com/study/2022/07/31/monte-carlo-simulation-napier/