【Python】モンテカルロ法でネイピア数eを推算してみた
以前、モンテカルロ法により円周率を推算する方法を調べて、実装した。
https://note.yu9824.com/study/monte-carlo-simulation-pi/
このとき、よく知られた無理数の定数のうちの一つであるネイピア数$e$はどうなんだろうと思った。
調べてみると結構面白かったので、簡単な証明を自分でしつつ、メモする。
モンテカルロ法によるネイピア数の推算
モンテカルロ法とは
Wikipediaによると以下。
シミュレーションや数値計算を乱数を用いて行う手法の総称。
簡単に言えば、ランダムに発生させた数値を使ってその値を求めることをいう。
よくこれを直感的にもわかりやすく説明するために、円周率$\pi$を推算する例が挙げられる。
推算のやり方
以下の方法で推算できるとのこと。
$[0,1]$区間の一様乱数（0と1の間に一様に分布した実数値確率変数）を独立にいくつも発生させて加えていくとき、その和が1を越えるまでにかかる乱数の個数の平均は、自然対数の底$e=2.71828\cdots$である。
この著者も書いているが、定義と全く関係のない設定から$e$が出てくるのがとても興味深いなと感じた。
簡単な証明
基本的にはこちらの文献を参考にした。
区間$[0,1]$上の独立な一様分布確率変数列を$X_1, X_2, X_3, \ldots$で表す。
一様分布の確率密度関数
一様分布の確率密度関数$f(x)$は以下の式で表される。
\[f(x) = \left\{ \begin{array}{ll} \frac{1}{1-0} = 1 & (0 \leq x \leq 1) \\ 0 & \mathrm{otherwise} \end{array} \right.\]参考: 連続一様分布1 | 統計学の時間
合計が$t$以下の確率の愚直計算
まず、$X_1$がある定数$t$ ($0 \leq t \leq 1$)以下になる確率$p(X_1 \leq t)$を求める。
\[p(X_1 \leq t) = \int_0^t f(x) \mathrm{d}x = \int_0^t 1\ \mathrm{d}x = t\]続いて、$X_1$と$X_2$の和が$t$以下の確率$p(X_1+X_2 \leq t)$を求める。
\[\begin{aligned} p(X_1+X_2 \leq t) &= \int_0^t p(X_1 \leq t-x)f(x) \mathrm{d}x \\ &= \int_0^t (t -x) \mathrm{d}x \\ &= \frac{1}{2}t^2 \end{aligned}\]同様に$X_1$と$X_2$, $X_3$の和が$t$以下の確率$p(X_1+X_2+X_3 \leq t)$を求める。
\[\begin{aligned} p(X_1+X_2+X_3 \leq t) &= \int_0^t p(X_1+X_2 \leq t-x)\ f(x) \mathrm{d}x \\ &= \int_0^t \frac{1}{2}(t - x)^2\ \mathrm{d}x \\ &= \frac{1}{6}t^3 \end{aligned}\]同様に$X_1$と$X_2$, $X_3$, $X_4$の和が$t$以下の確率$p(X_1+X_2+X_3+X_4 \leq t)$を求める。
\[\begin{aligned} p(X_1+X_2+X_3+X_4 \leq t) &= \int_0^t p(X_1+X_2+X_3 \leq t-x)\ f(x) \mathrm{d}x \\ &= \int_0^t \frac{1}{6}(t - x)^3\ \mathrm{d}x \\ &= \frac{1}{24}t^4 \end{aligned}\]合計が$t$以下の確率の一般項
係数の分母に着目すると、$1, 2, 6, 24$となっており、一般項が、$k!$となりそうな感じがしてくる（係数が引き継がれつつ、次数が上がってくることを考えれば4までやらなくても一般項が分かりそう）。
ここで、以下の仮定を置いてみる。
$X_1, X_2, X_3, \ldots, X_k$の和が$t$以下の確率$p(X_1+X_2+X_3+\ldots+X_k \leq t)$を求める式は以下の一般項で表される。
\[p(X_1+X_2+X_3+\ldots+X_k \leq t) = \frac{1}{k!}t^k\]先ほどまで行っていた愚直な計算のやり方を踏まえると帰納的に次の値を求められることがわかるので、帰納法による証明を試みる。
(i) $k = 1$のとき
先ほど示した通り。
(ii) $k=l\ (l \in \mathbb{N})$で仮定した関係式が成り立つとき、$k=l+1$のときに成り立つかを検証する。
$k = l$のときに成り立つので、以下の式が成立する。
\[p(X_1+X_2+X_3+\ldots+X_l \leq t) = \frac{1}{l!}t^l\]ここで、$l+1$の場合を求めると、
\[\begin{aligned} p(X_1+X_2+X_3+\ldots+X_l+X_{l+1} \leq t) &= \int_0^t p(X_1+X_2+X_3+\ldots+X_l \leq t - x)f(x) \mathrm{d}x \\ &= \frac{1}{l!} \int_0^t (t-x)^l\ \mathrm{d}x \\ &= \frac{1}{(l+1)!}t^{l+1} \end{aligned}\](i), (ii)より、すべての自然数に対して成り立つ。
この後の便宜のため、$k=0$のケースも考える。
0回目のサンプリングを行った後とは、まだサンプリングしていない状態（=合計は0）であるということになる。
したがって、$t$以下である確率は1になる。（$\because 0 \leq t$）
一般項に$t=0$を代入すると以下。
\[p(0 \leq t) = \frac{1}{0!}t^0 = 1\]このように$t=0$のときにも成り立つので$k$が0以上の整数であるときに成り立つ。
証明する命題に立ち返る
以上を踏まえて、最初の問題に戻る。今回の問題では$t=1$の場合を考えればよい。
はじめて$1$を超えるとは、言い換えると$k-1$回目までは、$1$を超えていなかったけれども、$k$回目になって初めて$1$を超えたといえる。
つまり、$k-1$回目に$1$より小さい確率から$k$回目に$1$より小さい確率を引けば良い。
$k$回目で初めて$1$を超える確率を$P(k)\ (k \in \mathbb{N})$とすると、これは以下の式で表される。
\[P(k) = p(X_1+X_2+X_3+\ldots+X_{k-1} \leq 1) - p(X_1+X_2+X_3+\ldots+X_{k-1}+X_k \leq 1)\]これを代入した上で整理すると、
\[\begin{aligned} P(k) &= \frac{1}{(k-1)!} - \frac{1}{k!} \\ &= \frac{k - 1}{k!} \end{aligned}\]よって、はじめて合計が1を超える回数の期待値$E$は、
\[\begin{aligned} E &= \sum_{k=1}^{\infty}k \times P(k) \\ &= \sum_{k=1}^{\infty} \frac{k(k-1)}{k!} \end{aligned}\]$k=1$の場合を特別視して、$\Sigma$から取り出して整理すると、
\[\begin{aligned} E &= 1 \times \frac{1\times0}{1!} + \sum_{k=2}^{\infty} \frac{k(k-1)}{k!} \\ &= \sum_{k=2}^{\infty} \frac{1}{(k-2)!} \end{aligned}\]わかりやすさのため、$n = k-2$と置くと以下のようになる。
\[E = \sum_{n=0}^{\infty} \frac{1}{n!}\]一方、ネイピア数$e$の指数関数$e^x$は、マクローリン展開より、以下の式で表される。
\[e^x = \sum_{n=0}^{\infty} \frac{1}{n!} x^n\]特に、$x=1$のとき、
\[e = \sum_{n=0}^{\infty} \frac{1}{n!}\]つまり、
\[e = E\]Pythonで実装
matplotlibを除いて標準ライブラリのみで実装した。
import random
import sys
import math
import itertools
from time import time
import matplotlib as mpl
import matplotlib.pyplot as plt
バージョン
print(f'Python: {sys.version}')
print(f'Matplotlib: {mpl.__version__}')
Python: 3.9.13 | packaged by conda-forge | (main, May 27 2022, 17:01:00)
[Clang 13.0.1 ]
Matplotlib: 3.5.2
再現性のためにシード値を固定する。
random.seed(334)
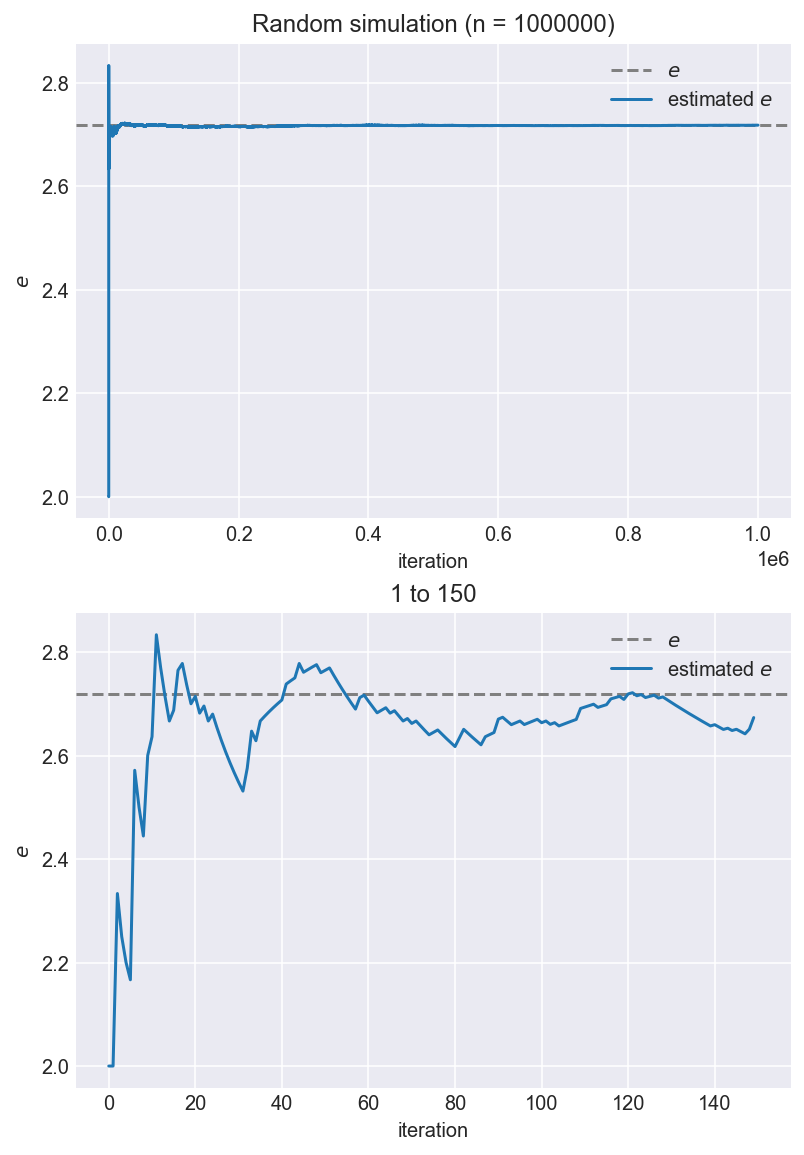
1,000,000回 （100万回）やってみる。
n_iteration = 1_000_000
# 時間測定
t1 = time()
lst_k = []
for iter in range(n_iteration):
x = 0
k = 0
while x <= 1:
x+=random.random()
k+=1
lst_k.append(k)
t2 = time()
print(f'Time: {t2-t1:.3f} sec')
Time: 0.474 sec
すぐ終わる。
# 累積和を利用してeを求める
lst_e_estimated:list[float] = [k_accumulated/(n_iter+1) for n_iter, k_accumulated in enumerate(itertools.accumulate(lst_k))]
# style
mpl.style.use('seaborn-darkgrid')
# figure, axisを生成
fig, axes = plt.subplots(2, 1, figsize=(6.4, 9.6), facecolor='w', dpi=144)
for j, _range in enumerate([(0, n_iteration), (0, int(n_iteration*0.00015))]):
ax:plt.Axes = axes[j]
# x軸の描画範囲を手動で設定するために計算
alpha = 0.05
offset = (_range[1] - _range[0]) * alpha
xlim = (_range[0] - offset, _range[1] + offset)
# 実際のeの値
ax.plot(xlim, [math.e]*len(xlim), c='gray', linestyle='--', label='$e$')
# 推算したeの値
ax.plot(range(*_range), lst_e_estimated[slice(*_range)], label='estimated $e$')
# layout
if j == 0:
ax.set_title(f'Random simulation (n = {n_iteration})')
else:
ax.set_title(f'{min(_range)+1} to {max(_range)}')
ax.set_xlim(xlim)
ax.set_xlabel('iteration')
ax.set_ylabel('$e$')
ax.legend()
fig.tight_layout()
print('実際の値: {:.5f}'.format(math.e))
print('推算値: {:.5f}'.format(sum(lst_k)/n_iteration))
実際の値: 2.71828
推算値: 2.71798
コメント
おそらく何かに役立つものではないと思うが、とても面白く、久しぶりに数学をやりたい気分だったので遊んでみた。
自分で上記のコードを動かせる方は収束の仕方が変わるのでシード値を変えて試してみると面白いと思う。
