NGBoostの確率解釈について
機械学習コンペなどで盛んに用いられる勾配ブースティングの一種として,Natural Gradient Boosting (NGBoost)がある.これは,「予測の不確かさ」を扱うことができるため,注目を浴びている.
NGBoostの解説記事自体はたくさん日本語でも存在するので,自分はこれに関連する論文や日本語の記事などを読んだが,それらの確率の取り扱いについての解釈がわからなかった(論文には詳しく書かれていないので当然である).
もちろんアルゴリズムを完全に理解できてはいないが,手法として取り入れるにあたって,この解釈は避けて通れないと考えた.
そこで色々探していると,論文のauthorが自ら,それらの解釈について言及している記事を見つけたので自分なりに日本語にしつつ,自分なりの解釈などのメモをとった.
筆者ら自身も,
確率的回帰については少し混乱があることも明らかになった.それは当然のことである.私たちは従来から利用されてきたものから少し離れているので,多少の混乱は当然である.だからこそ,私はこの記事を書いているのである.
NGBoost and Prediction Intervals - Towards Data Science
と言っており,解釈が難しいのだと思う.
なお,原文にはなかったが,判然としなかった用語にwikipediaのリンクを埋め込んだり,個人的に大事だと思ったことに対して太字装飾などを行った.
原記事のリンク:
https://towardsdatascience.com/interpreting-the-probabilistic-predictions-from-ngboost-868d6f3770b2
記事の目的
記事では,以下の2点にフォーカスして説明している.
- 回帰と分類の文脈で,教師付き学習と確率的教師付き学習の違い
- NGBoostのようなアルゴリズムで生成された予測区間
確率的な教師あり学習とNGBoost
まず,確率的教師あり学習とそれの対比となる「一般的な」教師あり学習について簡単な説明がある.
一般的な教師あり学習は,予測変数
これはとても馴染み深く,RandomForestRegressorなどの一般的な学習器は,ただ「私(機械学習モデル)的にはこれが1番いいと思ってます!」を返してくれるだけで,それに対してどれくらいの「自信」があってその値を返しているのかがわからないよね,ということを言っていると思われる.
同じ著者なので当然ではあるが,原著の論文のintroductionとかで書かれていた内容と関連しているように思われる.
続いて,確率的回帰や分類について以下のように述べている.
NGBoost以前は,柔軟なtreeベースのモデルで確率的回帰を行うことは困難であった.しかし,確率的な分類を行うことは,すでに長い間可能であった.
NGBoost and Prediction Intervals - Towards Data Science
これは,パーセプトロンの概念を勉強したときに理解した活性化関数sigmoid関数やsoftmax関数で聞いたことのある話だと思った.分類をするときに,出力される合計1の値を確率として捉えることができる,みたいな話.
NGBoostが追加したのは,確率的分類のアルゴリズムと同様に,高速で,使いやすく,柔軟性のある確率的回帰の方法である.
NGBoost以前にも確率的回帰は可能だったが,常にトレードオフの関係にあった.線形回帰は,同次性を仮定すれば確率的になるが,そうすると単純なモデルになってしまう.柔軟なノンパラメトリック手法が必要な場合,複雑なベイジアン手法は,その使用方法を理解し,マルコフ連鎖モンテカルロ 法を用いたsamplerを待つ時間があれば,常に選択肢の一つだった.一方,NGBoostは高速に動作し,さまざまな複雑なモデルをフィットさせることができる.
さらに最も重要なことに,箱から出してすぐに動作する.
NGBoost and Prediction Intervals - Towards Data Science
つまり,これまで確率的回帰は可能であったが,実行時間が長すぎることや構築の難しさ,モデルを単純にしないと使用できないなど,実用性が低かった.これをNGBoostは改善した,と私は解釈する.
予測区間とNGBoost
この記事の肝 (個人的には) となる文章がこれ.
早速であるが,NGBoostは信頼区間を返さない.
信頼区間「は」返さない.の方が,文脈を考えると正しいかもしれない.
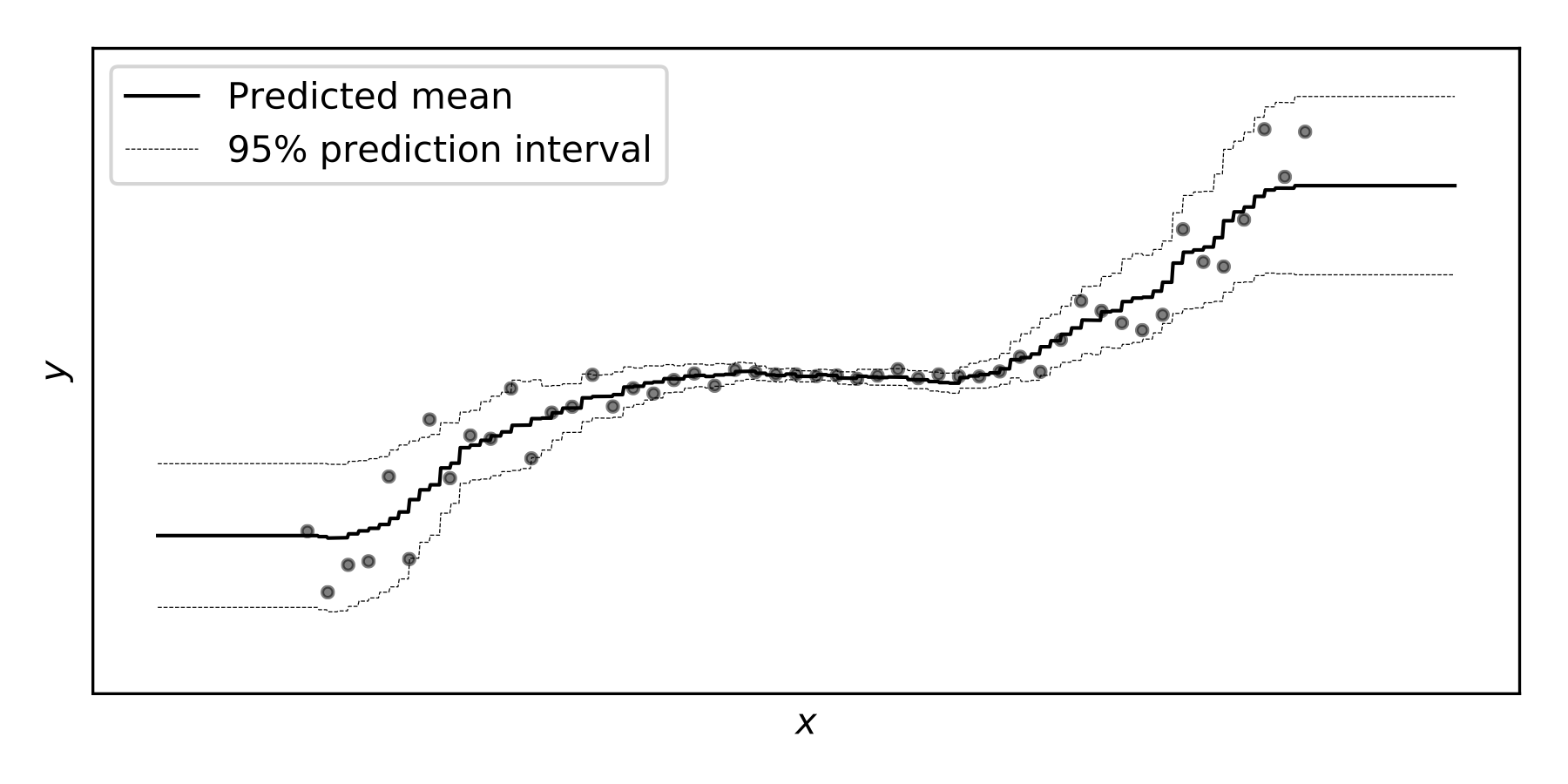
では,NGBoostのウェブサイトに掲載されているこの写真はどうなっているのか?確率的回帰の利点は信頼区間が得られることではないのか?
NGBoost and Prediction Intervals - Towards Data Science
この写真,とは以下の写真のこと.
NGBoost: Natural Gradient Boosting for Probabilistic Prediction
ここが,自分もわからなかったことで,この記事を読んで知りたかったこと.
筆者らはこれらの混乱の原因は「信頼区間」と「予測区間」を区別できていないことに起因するとして説明を続けている.
これらの違いについての著者らの説明はは以下のとおりである.
NGBoostでは,結果がそれぞれの可能な値をとる相対的な確率が得られる.この分布を操作すると(様々なセットで積分すると),モデルによれば
の確率で結果がその集合に入るような結果の集合を見つけることができる.しかし,それは信頼区間ではなく,結果の可能性の高い集合に過ぎない.
それが上の写真で見たものである.例えば,4つのクラス
があり,それらの推定確率( が与えられた場合)が, , , , だとする.集合 は の可能性のある結果の集合を形成する.これは,回帰の設定で を与えられた の密度の質量の を含む のような区間と同じである.これらのセットは一般的に「予測区間」と呼ばれている(ただし,それ自体が「区間」である必要はない). つまり,基本的にNGBoostが回帰の場合に返す予測区間は,代わりに標準的な確率的分類器を使って分類(おそらく別の問題)を行った場合に,自分で簡単に作成できるものである.
NGBoost and Prediction Intervals - Towards Data Science
著者は,説明のために分類の相対的な確率について持ち出している.私の解釈では,あくまで,この区間に95%の確率でこの区間に入ることを保証しているのではなく,このモデルは(今与えられたデータの傾向から推測すると)すべての考えうる結果の中で相対的に95%の確率でこの区間に入ると予測しているよ.くらいの感覚なのだと思う.
softmax関数やsigmoid関数を確率として解釈する感覚だと思えばいいのだと思っている.著者の言葉を使って言えば,これが「相対的な確率」なのだろうと想像する.
NGBoost は,モデルに基づいて各結果を観測する相対的な可能性を教えてくれるだけである.モデルを信じるならば,見たものがそのまま得られるのである.そうでない場合は,NGBoostの推定値にどの程度「自信がある」と考えるべきかを明確にするために,多くの追加の仮定を立てる必要がある.
NGBoost and Prediction Intervals - Towards Data Science
こういった文章からも,私は上記の解釈をした.
記事の結論
NGBoost が何をするのか,またその出力をどのように解釈すればよいのかについての混乱が解消されるとよいのであるが.理想的には,点推定 (point-estimation) のための教師付き学習と確率的教師付き学習を明確に区別できるようになり,予測区間の意味がわかるようになっていることである.
NGBoost and Prediction Intervals - Towards Data Science
従来の一般的な教師あり学習と確率的教師あり学習,および予測区間と信頼区間の違いをきちんと理解する必要があるということであろう.
私の解釈
文章の途中途中で挟んだが,最後にまとめる.
NGBoostが出力する確率は,相対的なものであり,信頼性を保証するものではない.あくまで,NGBoostのモデルを信頼する場合,この範囲に入るよ,くらい.
sigmoid関数やsoftmax関数の結果を確率と解釈する概念に近いのだと想像する.
予測区間と信頼区間をきちんと区別して解釈できるようになることが理解につながると思われる.
私の解釈や訳に惑わされたくないという方は元の記事をご参照ください(英語).
https://towardsdatascience.com/interpreting-the-probabilistic-predictions-from-ngboost-868d6f3770b2
付録: 信頼区間と予測区間の違いについて
「信頼区間と予測区間の違い」というサイトを参考に自分なりにメモをとってみる.
条件は参考先と同様に,10人分の成人男子の身長データ (つまり,
- 全国成人男性の平均身長(母平均)
- ある駅の階段を次に駆け上がってくる人の身長(次に観測される標本)
を推測したい場合について考える.先に結論を言うと,1. で求めた区間が信頼区間,2. で求めた区間が予測区間になる.
全国成人男性の平均身長(母平均)
よりわかりやすくするために,母平均
と表せる.
ある駅の階段を次に駆け上がってくる人の身長(次に観測される標本)
次に観測される標本は,母平均を推測した上で,それを元に分布を仮定して,再度その分布で起こりうる振れ幅を推測しなくてはならない.(したがって,推定の幅は広くなる.)
次に観測される標本のばらつき(分散)は,母平均のばらつき
つまり,次に観測される標本が今までの標本の観測を元に推測すると
なんか,こう考えるとわかる気がする.(気がするだけかも)
最後に
誤訳やこう解釈するべきなのではないかという意見等ある場合はぜひご教示いただきたいです.
参考リンク
- 原記事: NGBoost and Prediction Intervals - Towards Data Science
- 原著論文: Duan, T. et al. NGBoost: Natural Gradient Boosting for Probabilistic Prediction. (2019). arXiv:1910.03225
- 公式のGithub
- 公式のUser Gide
- 信頼区間と予測区間の違い